이번 페이지에서는 경사하강법의 접근법(?)에 대해서 설명한다.
설명의 편의를 위해서, w와 error를 익숙한 x와 y에 대한 식으로 변경하였다.
(참고로 수학적 증명은 없음!!)
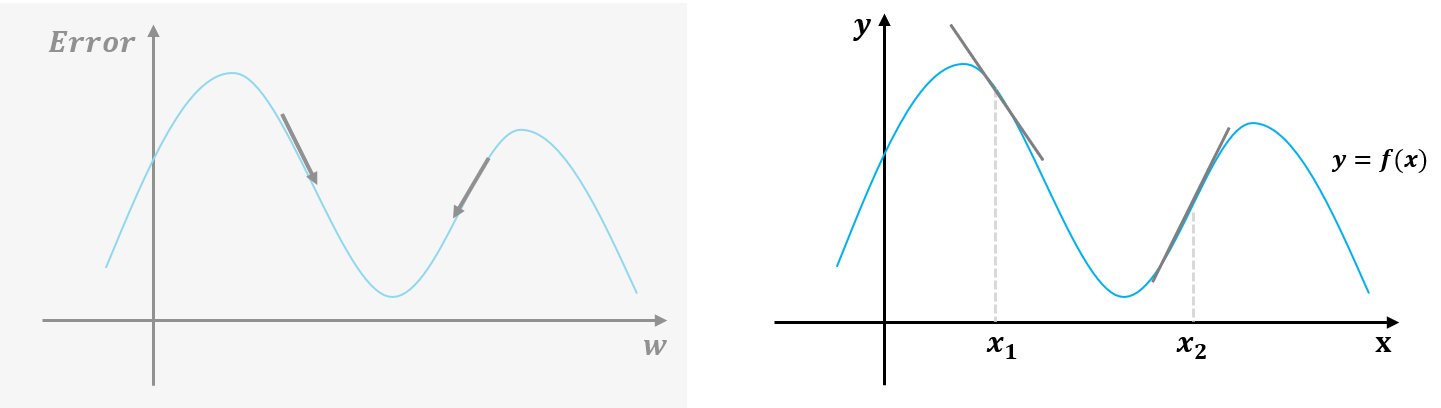
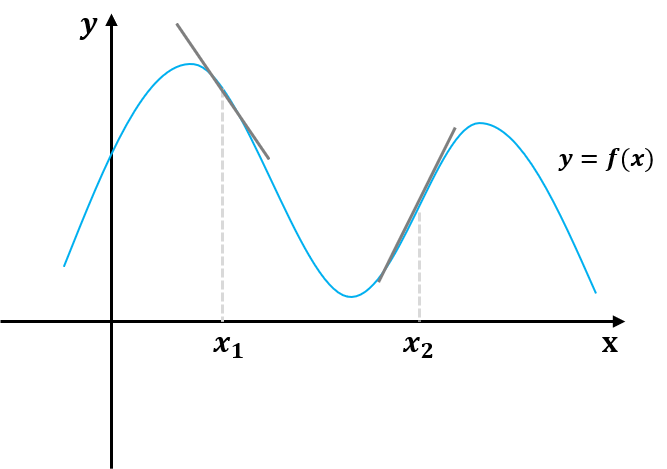
위의 식에서 y를 감소시키려면 x1과 x2를 어디로 보내야 할까?
정답은 x1은 오른쪽으로 x2는 왼쪽으로 조금씩 보내면 y의 값이 감소된다.
그렇다면 위와 같은 그림을 눈으로 확인하기 어렵다면 어떻게 x의 방향을 결정할 수 있을까?
정답은 기울기에 있다.
x1에서 기울기는 음(-)의 값을 가지고, x2에서 기울기는 양(+)의 값을 가진다.
- 기울기 = (y의 변화량)/(x의 변화량)
즉, x의 방향은 x에서의 기울기 값에 반대 방향으로 보내면 y를 작아지게 할 수 있다.
- x1에서 기울기가 음수이므로 x1은 양의 방향으로 이동
- x2에서 기울기가 양수이므로 x2는 음의 방향으로 이동
그럼 학습의 방향을 아래와 같은 식으로 나타낼 수 있다.
$x$ = $x$ -$\partial \over \partial x$$f(x)$
그런데 여기서 허점이 하나 있다. x2를 왼쪽으로 보내면 된다는 방향성은 위의 방법으로 찾을 수 있다.
하지만, 얼마를 보내야 할까?
만약 x2를 왼쪽으로 너무 많이 보내면 오히려 더 높은 위치의 y의 값을 가질 수도 있다.
그래서 여기에 $\alpha$의 값을 하나 곱해서 식을 완성한다.
$\alpha$는 learning size, learning step 등의 다양한 용어로 표현되기도 하는데, 여기서는 간단하게 x를 얼마만큼 변화시킬 것인가로 생각하면 좋을 것 같다.
$\alpha$까지 적용한 식을 표현하면 아래와 같다.
$x$ = $x$ -$\alpha$$\partial \over \partial x$$f(x)$
여기까지 왔으면, 경사하강법에 대한 개념적인 내용은 이해했다고 할 수 있을 것 같다.
이제 인공 신경망을 공부하면서 갑자기 등장하는 식에 당황하지 말자.
예) $\theta$ = $\theta$ -$\alpha$ $\partial \over \partial \theta$ $J\left(\theta\right)$
- $\theta$는 신경망의 매개변수(parameter)로 학습의 대상이 되는 값
- $J\left(\theta\right)$는 $\theta$에 대한 함수로 에러를 표현하는 함수
- $\alpha$는 어느 정도의 크기로 학습할 것인지
- 음(-)은 학습의 방향(에러를 줄이는 방향)이라고 이해하면 된다.
수공&열공!!!
'당당한 기계학습' 카테고리의 다른 글
| 의사결정나무 (Decision Tree) (1/3) (0) | 2021.01.21 |
|---|---|
| 분류 (Classification) (0) | 2021.01.15 |
| 코사인 유사도 (cosine similarity) (0) | 2021.01.15 |
| 경사하강법(Gradient descent) (1/2) (0) | 2021.01.09 |
| 인공신경망 활성화 함수(activation function)의 필요성 (0) | 2021.01.04 |